Tag: model order reduction
-

Multi-Objective Control Synthesis for Floating Wind Turbines
We are looking for a motivated and passionate student to contribute to our research in the field of wind energy and to work on a topic with strong scientific and industrial relevance. Floating wind turbines are complex systems, in which aerodynamics, hydrodynamics, structural dynamics, and control systems are strongly coupled. This multi-physics interaction makes the
-
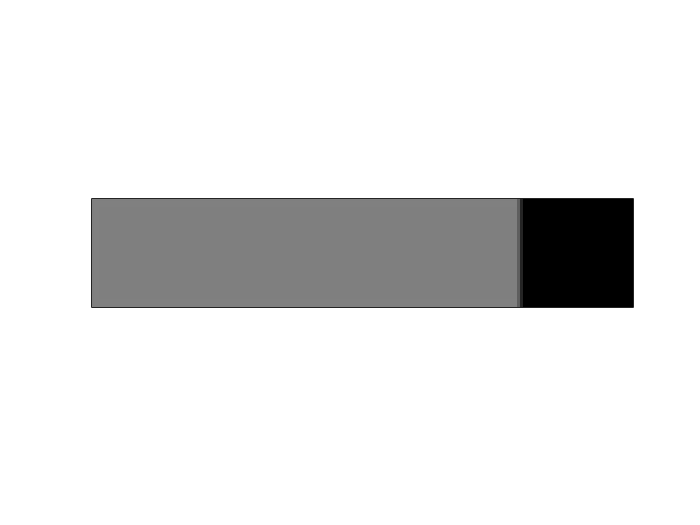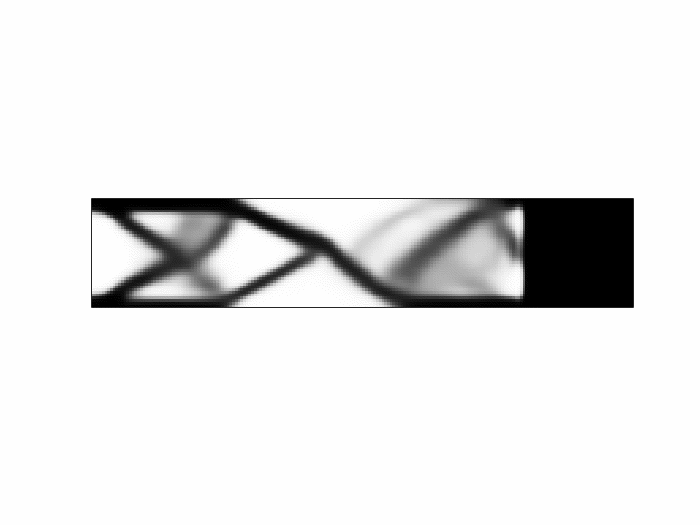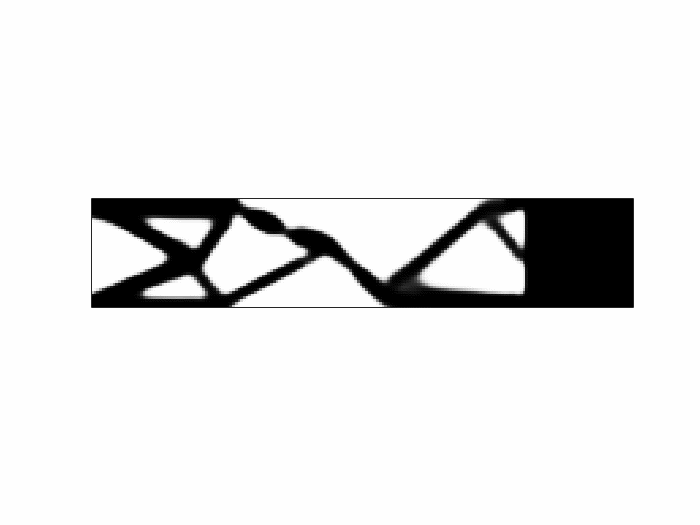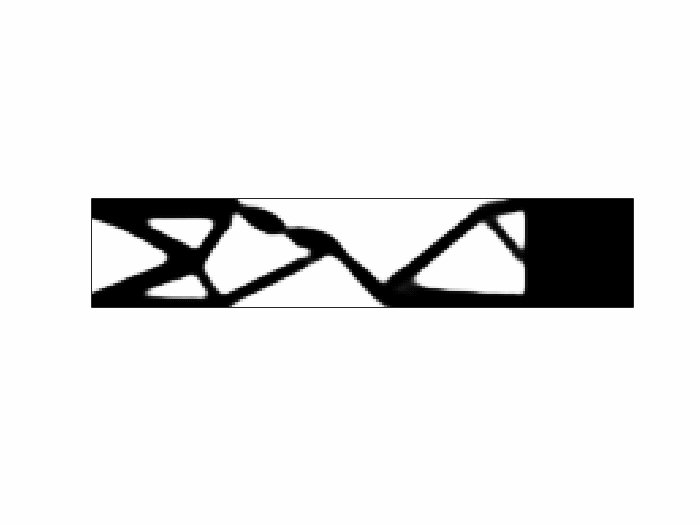
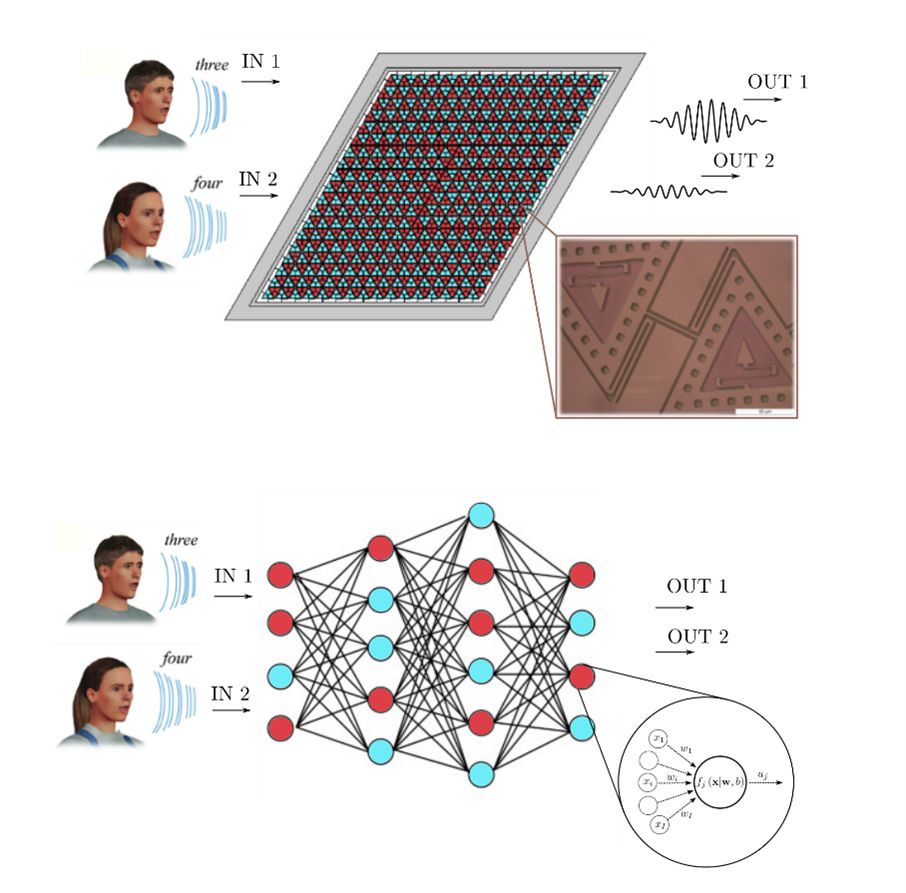
Topology Optimization in nonlinear dynamics: internal and parametric resonances
Topology optimization techniques for the design of MEMS devices in a linear dynamics framework have already been studied in several works in the literature. However, since there is no control of the degree of nonlinearity of the structure during the optimization process, the outcome of these routines often departs significantly from linearity. The consequence is
-
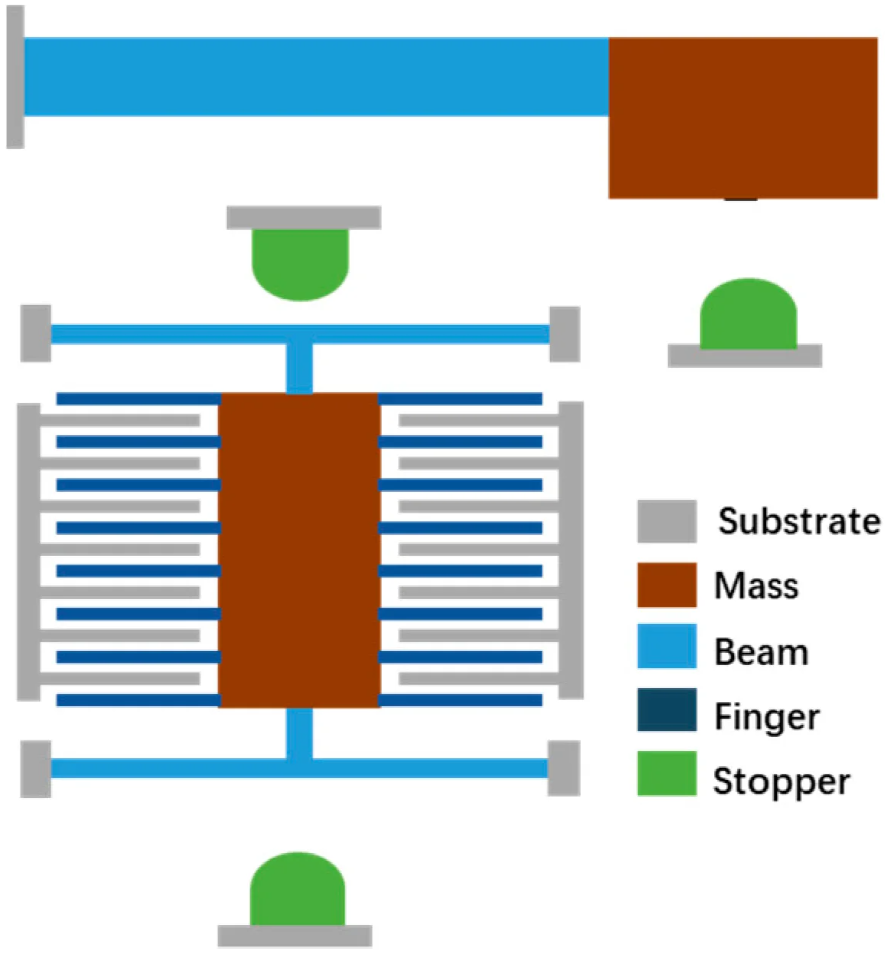
Mechanical nonlinearities (Geometric or Contact) in inertial MEMS sensors
Mechanical nonlinearities play an important role in inertial MEMS sensors and cannot be avoided. The trend to push the performance to the limits caused second-order nonlinear effects to become a critical phenomenon that must be considered: these effects are already visible and characterized on mass production devices. External shocks and vibrations could also induce other
-
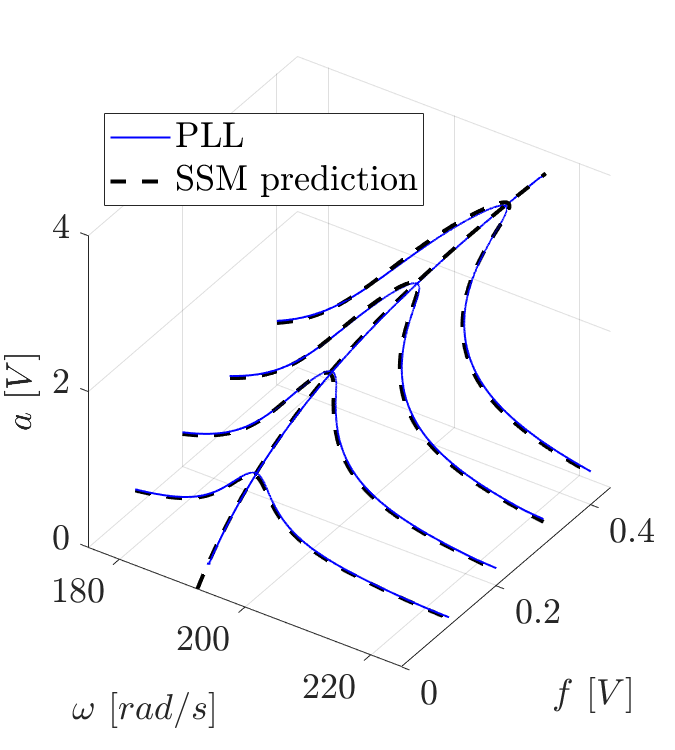
SSM-enhanced Control-Based Continuation (CBC)
In this project we aim to experimentally determine the backbone and the frequency response of a system using Control Based Continuation. CBC consists, loosely speaking, in creating a phase controller (PLL, Phase-Locked Loop) to lock a system at resonance (90°) and then extract the backbone by increasing the forcing with continuation algorithms, typical of numerical
-

Contact dynamics in inertial MEMS sensors
Nowadays, mechanical robustness is a key spec for inertial MEMS sensors. The contacts occurring in silicon structures are a relevant problem that may generate dangerous particles or even cause the breakage of the MEMS sensor. Despite these critical phenomena impacting the sensor’s manufacturing and lifetime functionality, the modeling approaches currently adopted are too simplified. The
-

Real-time optimal transport of robotic swarms in fluids in 3D domains
Optimally guiding large-scale swarms of drones, underwater vehicles or nanoparticles moving in a fluid is a crucial task in several fields, ranging from medicine to smart delivery. To steer the swarm dynamics avoiding obstacles, controllers must be able to rapidly adapt the optimal action to changes in the external environment, as often happen in applications.
-
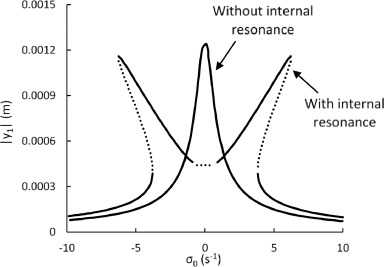
Optimization of systems with Internal Resonances
MEMS design is usually done following linear vibration theory, however, their real behavior often turns out to be nonlinear. To address this issue, our group developed optimization algorithms to target backbone curves, which are striclty connected to the nonlinearity of the vibration modes. As of now, the backbone computation can target only a single mode.
-
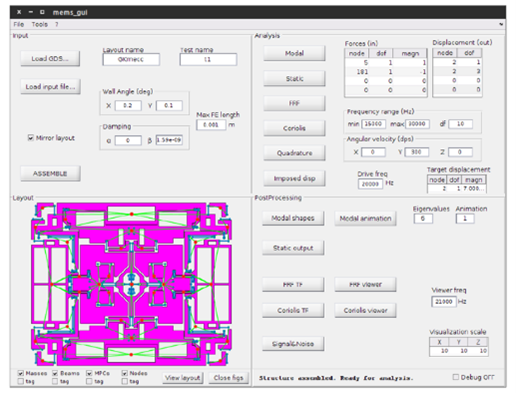
feMEMS: parametric optimization using semi-lumped parameter models
The design of MEMS devices usually involves several Finite Element (FE) analyses, each with different parameters (e.g. beam thicknesses) to tune the characteristics of the sensor. This trial-and-error procedure is tedious and time-consuming, even more so considering that typical FE models may count 100k-1M degrees of freedom. For this reason, our group developed a Matlab
-
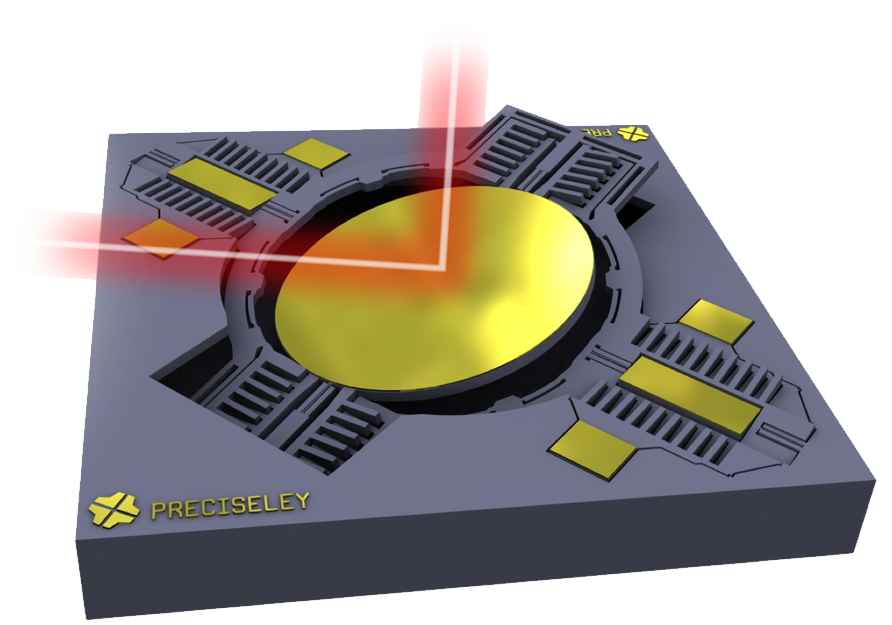
ROM for large rotations in a MEMS micromirror
MEMS micromirrors are micro components used to deflect light rays in many applications, such as to build projectors. Mainly due to their large rotations, these devices exhibit a nonlinear behavior that challenges the construction of traditional nonlinear Reduced Order Models. In this thesis, the candidate will investigate the subject of large rotations (moving on from