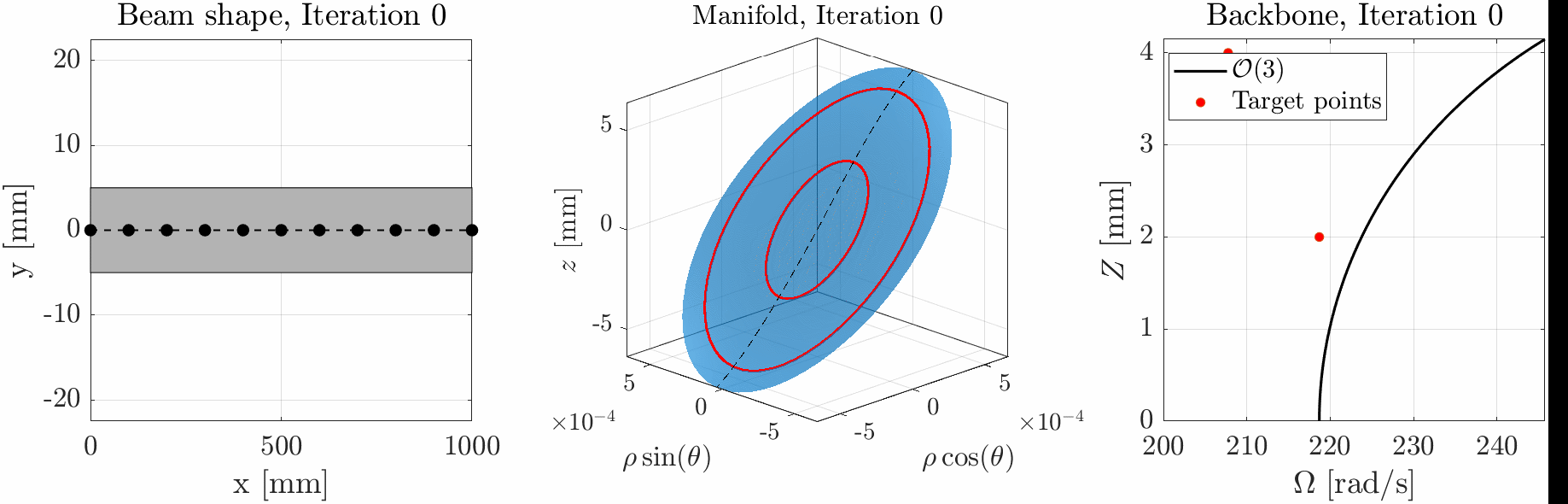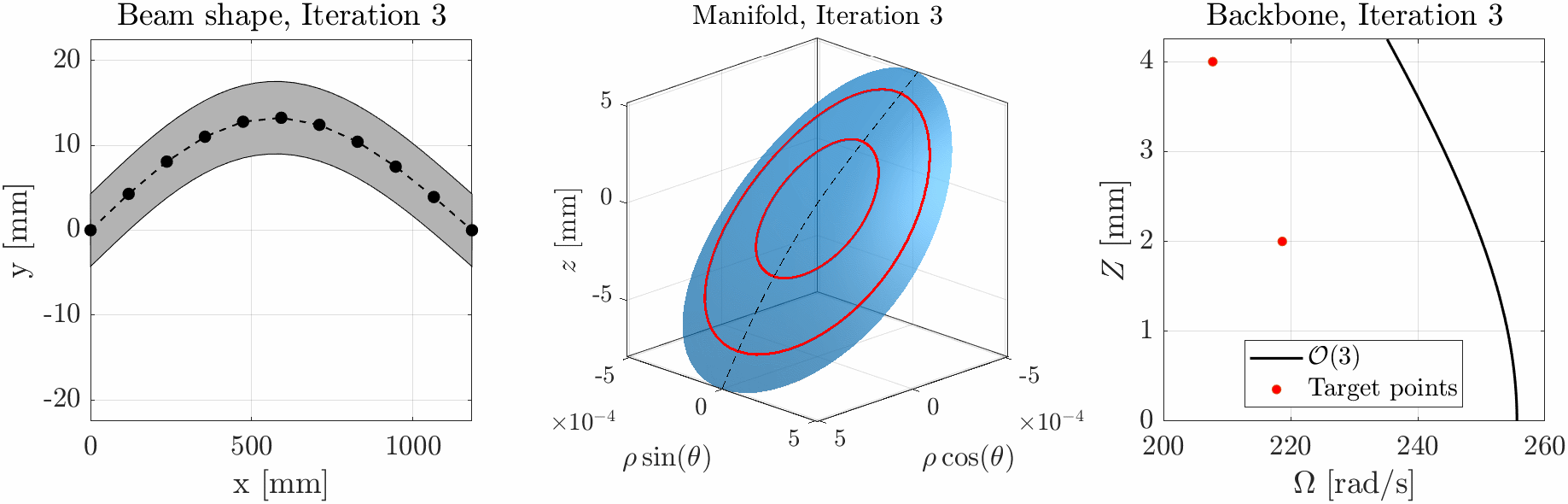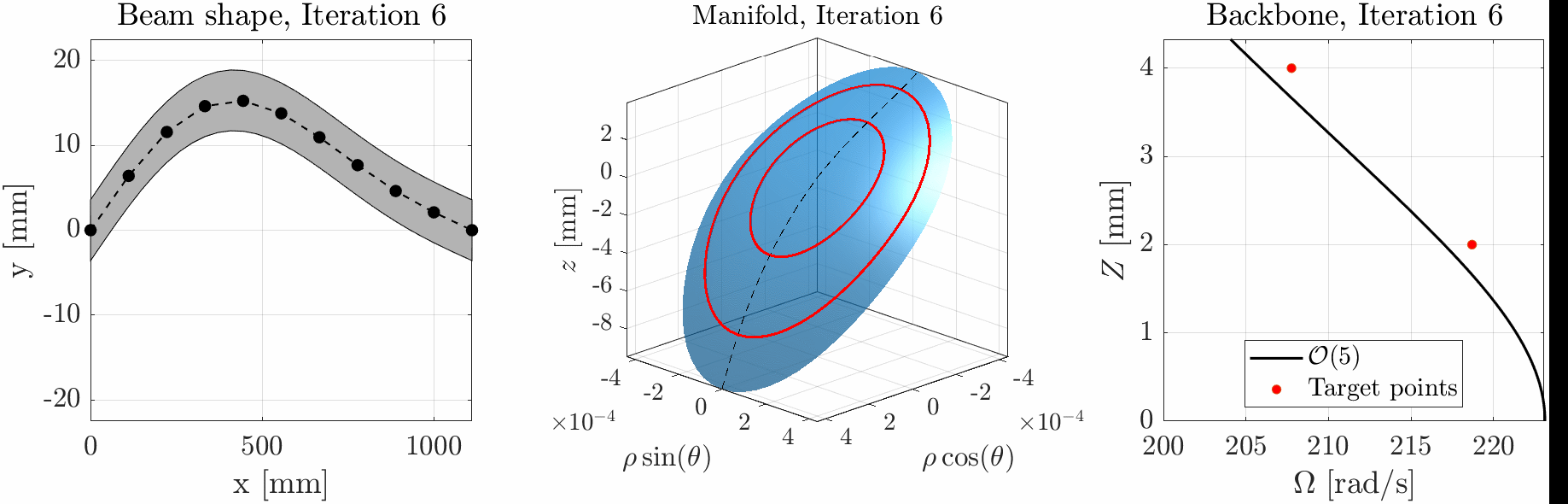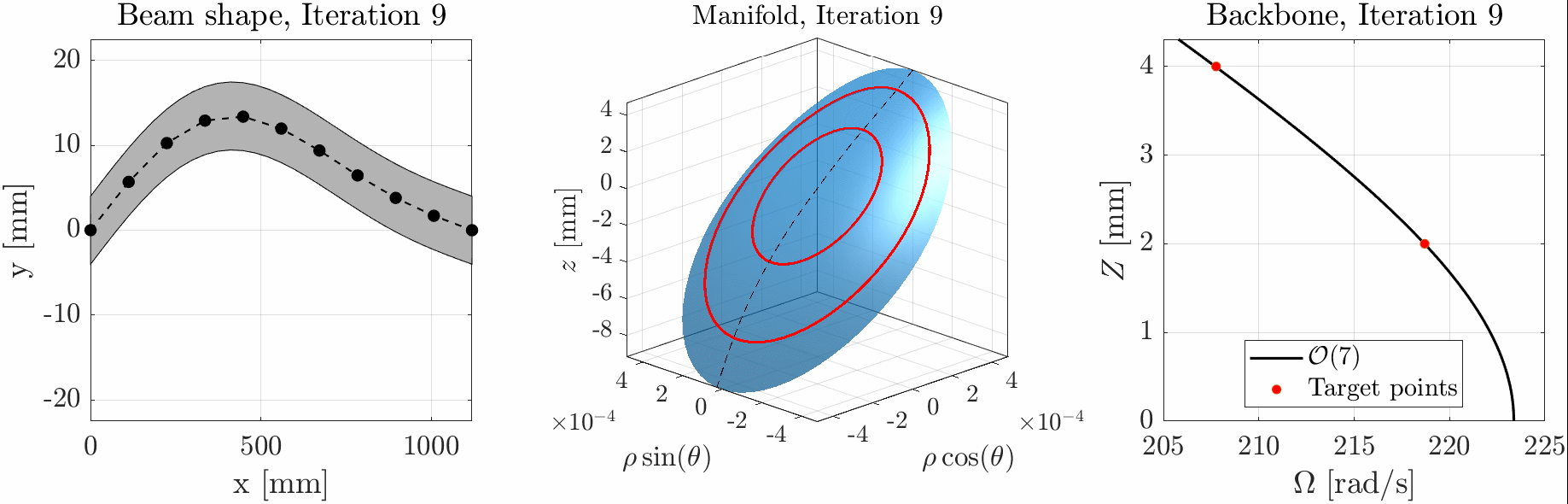
We have recently proposed a method to tailor the nonlinear response of a structure using Spectral Submanifolds (SSM, or Lyapunov Subcenter Manifolds – LSM) and an optimization procedure1. By defining a set of frequency-amplitude pairs we can fit the backbone curve of the system to these points. The computation of the sensitivities of the LSM, required for the optimization procedure, is still very cumbersome and computationally demanding, reason why this approach is still limited to low-dimensional models with a low number of parameters. To remove this constraint, the adjoint method can be used to compute the sensitivity with respect to the design parameters all together, rather than one by one. This effectively allows to use a very high number of parameters without affecting the computational cost of the optimization.
At the time being, the adjoint formulation has been developed for SSM up to the third order2. This entails some limitations. The aim of this project is to extend the adjoint formulation to handle arbitrary expansion order of the SSM and to apply it to a relevant numerical example.
At the time being, the adjoint formulation has been developed for SSM up to the third order2. This entails some limitations. The aim of this project is to extend the adjoint formulation to handle arbitrary expansion order of the SSM and to apply it to a relevant numerical example.
References
- Pozzi, M., Marconi, J., Jain, S. et al. Backbone curve tailoring via Lyapunov subcenter manifold optimization. Nonlinear Dyn 112, 15719–15739 (2024). https://doi.org/10.1007/s11071-024-09881-5
- Li, M. Explicit sensitivity analysis of spectral submanifolds of mechanical systems. Nonlinear Dyn 112, 16733–16770 (2024). https://doi.org/10.1007/s11071-024-09947-4
