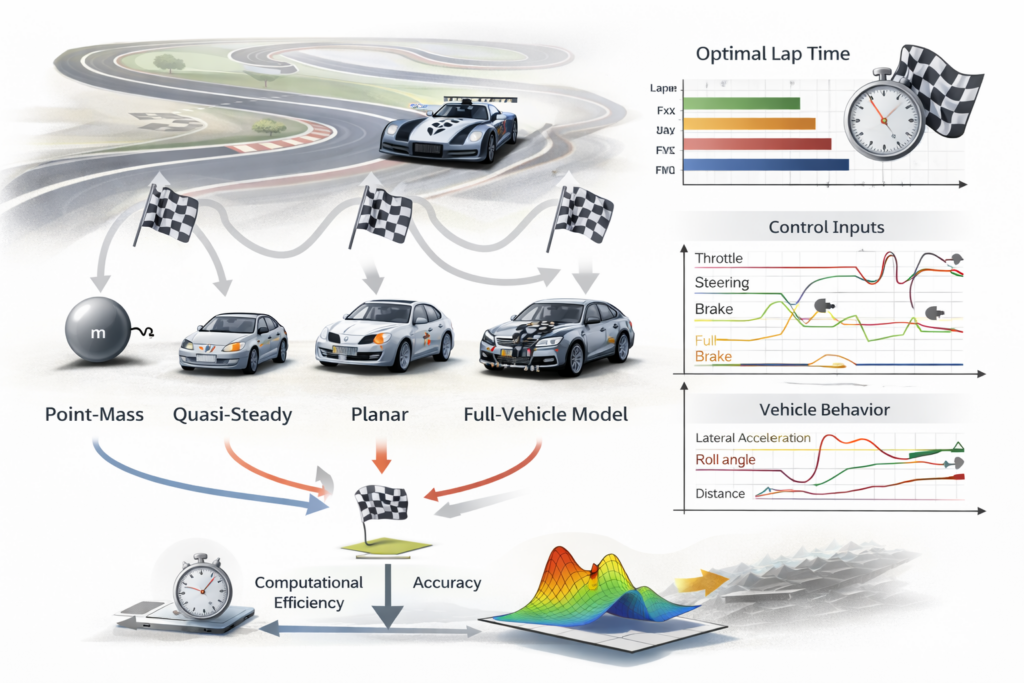
This thesis focuses on the study of the influence of different vehicle dynamic models on lap time optimization, with particular attention to how model fidelity affects optimal control solutions and predicted vehicle performance. Lap time optimization is a central topic in motorsport engineering and high-performance vehicle development, where numerical simulation and optimal control techniques are extensively used to support design choices, setup decisions, and control strategy development. However, the level of detail required in vehicle modeling to achieve reliable results while maintaining acceptable computational cost remains an open and practically relevant question.
The work investigates and compares various vehicle modeling approaches commonly adopted in lap time simulations. These range from simplified point-mass and quasi-steady models, which describe the vehicle as a lumped mass subject to simplified force constraints, to more advanced planar models that include yaw dynamics, load transfer, and tire nonlinearities. When feasible, the study may also consider full-vehicle dynamic representations that account for roll dynamics, suspension effects, and coupled longitudinal–lateral behavior. Each modeling approach is formulated within an optimal control framework and used to solve a lap time optimization problem over a given circuit.
The primary objective of the thesis is to assess how the choice of vehicle dynamic model influences the predicted optimal lap time, the resulting control inputs (such as throttle, braking, and steering actions), and the overall vehicle behavior along the track. Particular emphasis is placed on identifying discrepancies in cornering strategies, braking points, and acceleration phases that arise when different model fidelities are employed. The sensitivity of the optimal solution to modeling assumptions, including tire force representations and load transfer effects, is also analyzed.
From a methodological perspective, the thesis combines vehicle dynamics modeling, optimal control theory, and numerical optimization techniques. State-of-the-art solvers for trajectory optimization may be employed to handle the resulting nonlinear optimal control problems. Computational efficiency, convergence robustness, and numerical stability are evaluated alongside the accuracy of the physical predictions.
The results of the study are expected to highlight the trade-off between computational cost and model accuracy, providing quantitative insights into when simplified models are sufficient and when higher-fidelity representations are necessary. The outcomes will offer practical guidelines for selecting appropriate vehicle models in performance-oriented simulations, lap time prediction tools, and motorsport applications, supporting both academic research and industrial practice.
Contacts: michele.vignati@polimi.it, mattia1.belloni@polimi.it, veronica.deguglielmo@polimi.it
