Automotive suspension systems play a fundamental role in determining vehicle ride comfort, road holding, and overall handling performance. Modern vehicles operate over a wide range of driving conditions in which suspension components exhibit significant nonlinear behavior due to geometric effects, nonlinear stiffness characteristics, damping properties, and the interaction with road irregularities. The aim of this Master’s thesis is to study the nonlinear dynamic behavior of automotive suspension systems and to develop optimization strategies to improve vehicle performance.
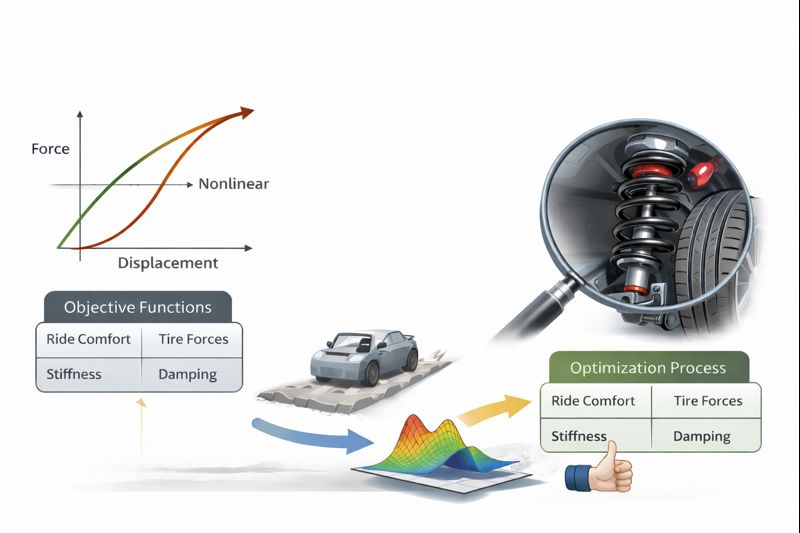
The thesis will focus on the modeling, analysis, and optimization of suspension dynamics using nonlinear dynamic methods. A detailed suspension model will be developed, considering either a quarter-car, half-car, or full-vehicle configuration depending on the desired level of complexity. Nonlinearities arising from springs, dampers, bushings, bump stops, and suspension kinematics will be explicitly included in the model. Tire–road interaction models suitable for vertical dynamics will also be considered to capture realistic excitation conditions.
The equations of motion will be derived using appropriate analytical or numerical techniques, such as Lagrange’s formulation or multibody dynamics approaches. The nonlinear dynamic response of the system will be investigated through time-domain simulations under different road profiles, including deterministic inputs (e.g., bumps, sine waves) and stochastic excitations representing real road roughness. Special attention will be paid to the influence of nonlinear effects on ride comfort, suspension travel, and tire load variation.
To gain deeper insight into system behavior, nonlinear analysis tools such as phase-space representations, frequency response analysis, and bifurcation analysis may be employed. These techniques will be used to identify critical operating conditions, dynamic instabilities, or performance degradation associated with nonlinear phenomena.
Based on the developed model, an optimization framework will be implemented to improve suspension performance. Objective functions may include ride comfort indices, handling-related metrics, and constraints on suspension deflection and tire forces. Optimization variables may involve suspension stiffness and damping characteristics, geometric parameters, or nonlinear component properties. Both gradient-based and heuristic optimization methods may be explored.
The expected outcome of this thesis is a comprehensive understanding of how nonlinear dynamics influence suspension performance and how these effects can be exploited or mitigated through systematic optimization. The results will provide valuable insights for the design and tuning of advanced automotive suspension systems, contributing to improved vehicle comfort, safety, and performance
Contacts: michele.vignati@polimi.it, mattia1.belloni@polimi.it
Where: PoliMi
Duration: expected 9 months
